Research

Rayan (Ray) Ibrahim
Visiting Assistant Professor,
Department of Mathematics,
Lafayette College

Publications and Preprints

  1. Determinants of Simple Theta Curves. Link
    Journal of Knot Theory and Its Ramifications, with M. Elpers, A. H. Moore. Accepted.
  2. Bootstrap Percolation, Connectivity, and Graph Distance. Link
    The Art of Discrete and Applied Mathematics, with H. LaFayette, K. McCall. Accepted.
  3. Introducing 3-Path Domination. Link
    Journal of Combinatorial Mathematics and Combinatorial Computing (2024), with E. King, R. Jackson.
  4. Submesoscale Kinematic Properties in Summer and Winter Surface Flows in the Northern Gulf of Mexico. Link
    Journal of Geophysical Research: Oceans (2020), with M. Berta, A. Griffa, A. C. Haza, J. Horstmann, H. S. Huntley, B. Lund, T. M. Özgökmen, A. C. Poje.

In Preparation

  1. Minimum 2-Percolating Sets in 2-Connected, Diameter 2 Graphs. Link
    with H. LaFayette, K. McCall. Submitted.
  2. \(2\)-Neighbor Bootstrap Percolation and Forbidden Induced Subgraphs
    In Preparation.
  3. \(r\)-Neighbor Bootstrap Percolation: Complementary Prisms and Bounds
    In Preparation.

Research Interests

Below you will find some of my interests and projects. My research interests are primarily graph theory (extremal and structural), applications of graph theory (e.g. to the natural sciences), and the intersection of combinatorics and topology.

My dissertation: Problems in Graph Theory With Applications to Topology and Modeling RNA

Bootstrap Percolation

A graph becoming infected
Bootstrap Percolation is a process defined on a graph which begins with an initial set of infected vertices \(A_0\) and threshold \(r\). In each subsequent round, an uninfected vertex becomes infected if it is adjacent to at least \(r\) previously infected vertices. If \(A_0\) begins a process in which every vertex of the graph eventually becomes infected, then we say that \(A_0\) percolates. A graph is \(r\)-Bootstrap-Good (or \(r\)-BG) if it contains a percolating set of size \(r\) (the minimum number of vertices needed to infect the entire graph is equal to the threshold.) Above, there is an example of a \(2\)-BG graph.

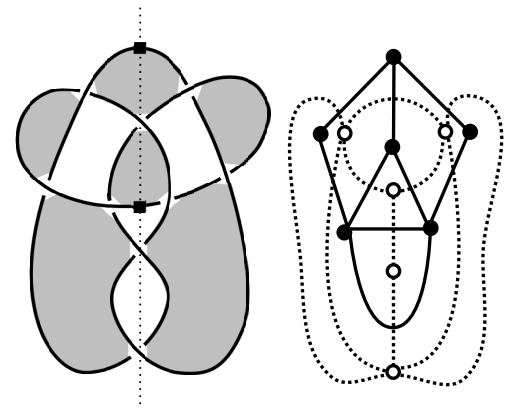
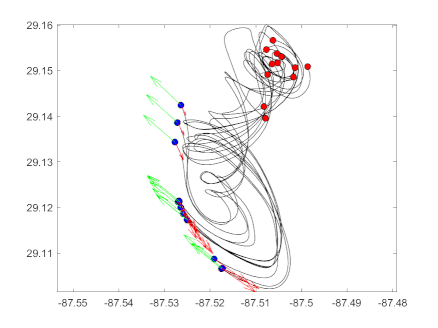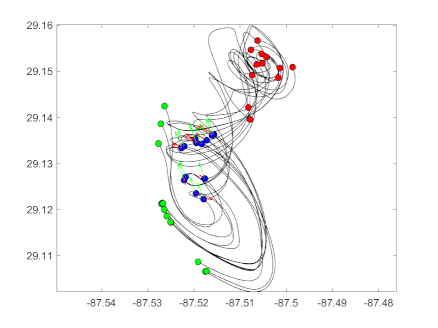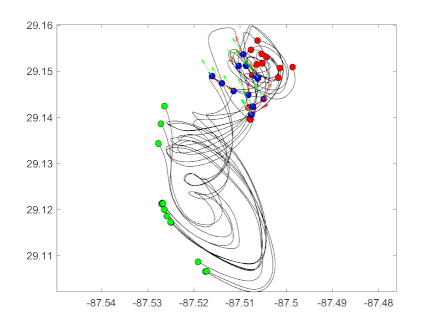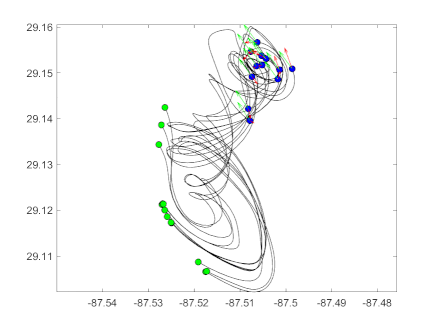
Graph Independence

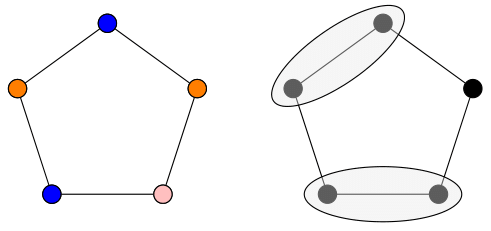
The five cycle with coloring and minor shown.
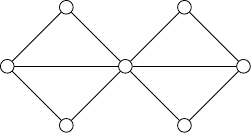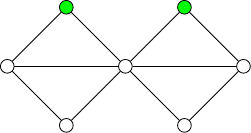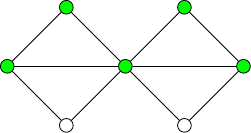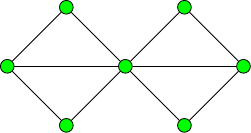
Let \(G = (V,E)\). A set \(I\subseteq V(G)\) is an independent set (or stable set) if no two vertices in \(I\) are connected by an edge. The independence number of \(G\), denoted \(\alpha(G)\) is the maximum size of an independent set. Graphs with independence number one are the complete graphs (graphs in which every pair of vertices is connected by an edge.) The graphs which have independence number two are precisely the complements of triangle-free graphs. Although they are one step above independence number one graphs so to speak, their structure can vary wildly. Independence number two graphs are of particular interest when it comes to Hadwiger's Conjecture. See this survey by Paul Seymour.

Topology and Graph Theory

A theta curve is a spatial embedding of the \(\theta\)-graph in the three-sphere, taken up to ambient isotopy. One can define the determinant of a theta curve as an integer-valued invariant arising from the first homology of its Klein cover. When a theta curve is simple, containing a constituent unknot, one can prove that the determinant of the theta curve is the product of the determinants of the constituent knots. This can be done entirely using combinatorial methods. Here are two papers with (very cool) results used in our proof.

Oceanography

A drifter cyclone event.
If I were to have a midlife crisis, and consider pivoting from my current interests, I would probably dive into oceanography (the pun is intended.)